Ángulo entre dos rectas en el espacio

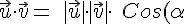El ángulo que forman dos rectas en el espacio, viene dado por el ángulo que forman sus vectores de dirección. Su cálculo es sencillo a partir del producto escalar, pues $\vec{u}\cdot\vec{v}=\;|\vec{u}|\cdot|\vec{v}|\cdot\;Cos(\alpha)\;\Rightarrow\;Cos(\alpha)=\frac{\vec{u}\cdot\vec{v}}{|\vec{u}|\cdot|\vec{v}|}$ .
Ahora bien, si elegimos dos vectores al azar se pueden obtener dos ángulos distintos que son suplementarios (α+β=180º). Como entre ángulos suplementarios se verifica que Cos(α)=-Cos(180-α), si en la fórmula anterior tomamos valores absolutos siempre obtendremos el coseno del menor ángulo que forman dos rectas, basta con $\;Cos(\alpha)=\|\frac{\vec{u}\cdot\vec{v}}{|\vec{u}|\cdot|\vec{v}|}\|$ para obtener el mismo coseno independientemente de los vectores elegidos.
El ángulo será $\;\alpha=ArcCos\|\frac{\vec{u}\cdot\vec{v}}{|\vec{u}|\cdot|\vec{v}|}\|$

Sean las rectas $r=\left{3x+y-z-2\;=\;0\\7x+y-3z\;=\;0$ $s=\frac{x+1}{-1}=\frac{y}{-1}=\frac{z-1}{1}$
Determina el ángulo que forman.

Lo primero que haremos será determinar el vector director de cada una de ellas. Si la ecuación de la recta está en forma vectorial, su vector de dirección es "el que multiplica al parámetro". Si está en forma paramétrica los coeficientes del parámetro nos dan ese vector. Si está en forma continua, el vector vendrá dado por los denominadores de las igualdades y finalmente si está en forma implícita o general, el vector director se determina con producto vectorial de los vectores normales de los planos que la determinan.

En este caso los vectores directores de las rectas r y s son respectivamente $\vec{u}=(1,-1,2)\;y\;\vec{v}=(-1,-1,1)$
$\vec{u}\cdot\vec{v}\;=\;u_1\cdot\;v_1\;+\;u_2\cdot\;v_2\;+\;u_3\cdot\;v_3\;\Rightarrow$

$\vec{u}\cdot\vec{v}=2$

$\fs2|u|\;=\;\sqrt{u_1^2+u_2^2+u_3^2}\simeq2.45$

$|v|\;=\;\sqrt{v_1^2+v_2^2+v_3^2}\simeq1.73$

$Cos(\alpha)=\|\frac{\vec{u}\cdot\vec{v}}{|\vec{u}|\cdot|\vec{v}|}\|=\;\|\frac{2}{2.45\cdot1.73}\|\;=\;0.47\;\Rightarrow$

$Arcos(\alpha)=61.87^o$

Halla el ángulo que forman las rectas $r=(x,y,z)=(0,0,-4)+\lambda(0,3,8)$ $s=\left{8x+6y+9z-12\;=\;0\\5x-3y+9z-21\;=\;0$ .

Nota: Expresa el ángulo en grados y lo redondeas a dos cifras decimales, para ello debes arrastrar más decimales en el redondeo de los módulos porque de lo contrario aumenta mucho el error

Solucion: El ángulo es de º