Ecuaciones del plano
Ecuación vectorial
Si se conoce un punto

de un plano y dos vectores de dirección

, se pueden determinar todos sus puntos, a la identificación de esos puntos se le conoce como ecuación del plano.
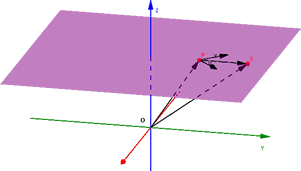
Un punto cualquiera del plano

viene determinado por su vector de posición

, como conocemos

, su vector de posición será

.
Es claro que

, al estar

y

en el plano,

es un vector de dirección del plano, como

y

son dos vectores directores entonces

es combinación lineal de

y

, es decir, existen

y

tal que

.
Luego la ecuación vectorial del plano es

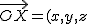\;\vec{OP}=(p_1,p_2,p_3))
\;\vec{v}=(v_1,v_2,v_3))
=(p_1,p_2,p_3)+\lambda(u_1,u_2,u_3)+\mu(v_1,v_2,v_3))
Por tres puntos no alineados siempre pasa un plano. Halla la ecuación vectorial del plano que pasa por los puntos P(1,2,3), Q(-1,0,2) y R(0,0,1)
Para hallar la ecuación necesitamos un punto y dos vectores de dirección. Como P y Q son dos puntos del plano, el vector

será un vector director, hacemos lo mismo con P y R

.
\;\;\vec{PR}=(-1,-2,-2))
Así la ecuación vectorial del plano es
=(1,2,3)+\lambda(-2,-2,-1)+\mu(-1,-2,-2))